【R语言】GARCH模型的应用 |
您所在的位置:网站首页 › r语言 ma模型 › 【R语言】GARCH模型的应用 |
【R语言】GARCH模型的应用
|
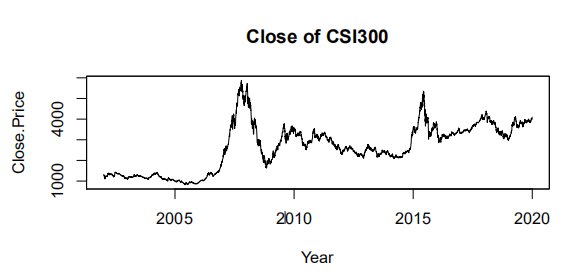
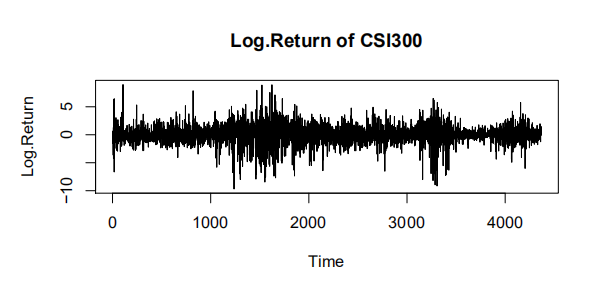
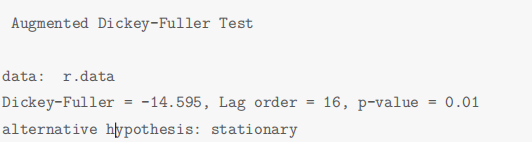
本文是时间序列分析课程的作业,基于R、Rnw和Latex进行编写。 GARCH代码实现主要参考自《经济与金融计量方法:原理、应用案例及R语言实现》和对应包的官方文档,代码进一步整合,但每次执行时可能需要较长的时间,建议执行完后将结果导出成excel。如果本文存在问题,随时欢迎交流~ 一、数据来源沪深300指数,是由沪深证券交易所于 2005 年 4 月 8 日联合发布的反映沪深 300 指数编制目标和运行状况的金融指标,并能够作为投资业绩的评价标准,为指数化投资和指数衍生产品创新提供基础条件。因此,本次数据来源于网易财经,研究的数据集对象是沪深 300 指数(股票代码为000300),此次分析选取了沪深 300 指数2000 年1月到2019年12月的工作日收盘价格数据。 二、数据分析 (一)时序图 为了分析数据的波动情况,对其进行对数化和差分得到对数收益率,下图为沪深 300 指数的收盘价时序图和对数收益率时序图。 Augmented Dickey-Fuller Test (ADF) 是 DF 检验的拓展形式,可以对存在高阶滞后的序列进行单位根检验,原假设存在单位根,即序列不平稳。本文使用adf.test()进行单位根检验,检验结果如下所示,p 值远小于 0.01 说明拒绝原假设,即序列是平稳的。 序列平稳后,使用auto.arima()对序列自动识别均值模型。 识别出来的模型为ARMA(4, 4)。经过模型识别后,对模型 A R M A ( 4 , 4 ) ARMA(4,4) ARMA(4,4)进行参数显著性检验。检验结果发现部分参数不显著,采用建立疏系数的均值模型,将不显著的参数强制为0。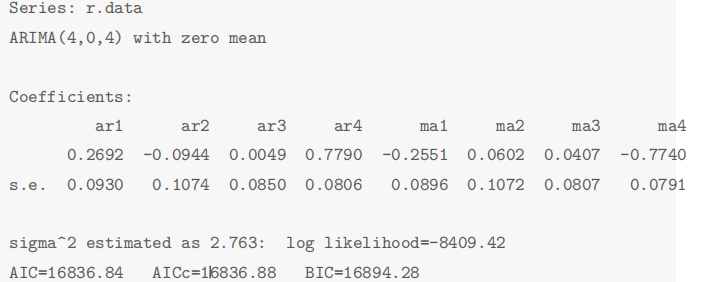 采用疏系数的
A
R
M
A
ARMA
ARMA模型后的参数显著性检验结果来看,非零参数结果都显著。(注:这一步存有疑问,后续依旧是采用
A
R
M
A
(
4
,
4
)
ARMA(4,4)
ARMA(4,4)的非疏系数模型进行拟合) 采用疏系数的
A
R
M
A
ARMA
ARMA模型后的参数显著性检验结果来看,非零参数结果都显著。(注:这一步存有疑问,后续依旧是采用
A
R
M
A
(
4
,
4
)
ARMA(4,4)
ARMA(4,4)的非疏系数模型进行拟合) 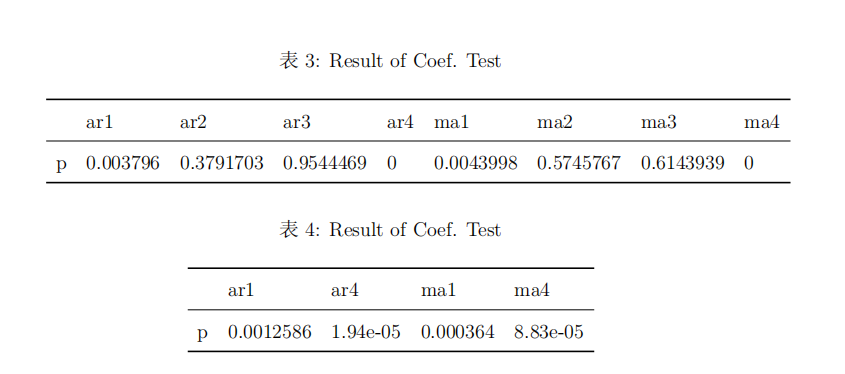 (二)方差模型建立
1. ARCH效应检验
(二)方差模型建立
1. ARCH效应检验
上述建立模型后,对残差进行ARCH效应检验。Ljung-Box统计量 Q ( m ) Q(m) Q(m)对残差序列进行自相关检验。原假设是序列不存在自相关,在残差的平方序列中可以检验条件异方差。 使用MTS包中的archTest()进行检验 检验结果显示,滞后10阶和滞后20阶的残差序列存在自相关,因此拒绝原假设,残差序列存在ARCH效应。## [1] "m = 10" ## Q(m) of squared series(LM test): ## Test statistic: 1043.197 p-value: 0 ## Rank-based Test: ## Test statistic: 849.5804 p-value: 0 ## [2] "m = 20" ## Q(m) of squared series(LM test): ## Test statistic: 1705.592 p-value: 0 ## Rank-based Test: ## Test statistic: 1565.588 p-value: 0 2. 标准GARCH模型建立上述ARCH效应表明,条件方差是依赖于过去值。因此可以考虑GARCH模型对方差方程进行参数估计。 使用tseries包中的garch()函数进行拟合标准GARCH模型。 从结果上看,拟合出来的参数都显著,Box-Ljung test结果中的P值大于显著性,因此可以认为模型的残差无序列相关,说明该模型拟合效果较好。但实际上,其中Jarque Bera Test用于对回归残差的正态性进行检验,Shapiro - Wilk Normality Test也可以用于正态性检验,原假设都是是残差序列服从正态分布,检验结果表明,残差序列是不服从正态分布,因此可以对模型进行优化,考虑其他GARCH模型。## Call: ## garch(x = r.data, order = c(1, 1)) ## ## Model: ## GARCH(1,1) ## ## Residuals: ## Min 1Q Median 3Q Max ## -4.91948 -0.53035 0.04107 0.57992 5.60582 ## ## Coefficient(s): ## Estimate Std. Error t value Pr(>|t|) ## a0 0.011014 0.002491 4.422 9.78e-06 *** ## a1 0.063407 0.004076 15.556 < 2e-16 *** ## b1 0.934953 0.003839 243.530 < 2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Diagnostic Tests: ## Jarque Bera Test ## ## data: Residuals ## X-squared = 659.37, df = 2, p-value < 2.2e-16 ## ## ## Box-Ljung test ## ## data: Squared.Residuals ## X-squared = 1.5224, df = 1, p-value = 0.2173 四、模型优化 (一)模型拟合上述的模型考虑的是 A R I M A ( 0 , 0 , 0 ) ARIMA(0,0,0) ARIMA(0,0,0)的标准 G A R C H ( 1 , 1 ) GARCH(1,1) GARCH(1,1)模型,即均值模型的参数均设置为0。而从均值模型的分析来看,可以拟合 A R I M A ( 4 , 0 , 4 ) ARIMA(4,0,4) ARIMA(4,0,4)的均值模型与 G A R C H ( 1 , 1 ) GARCH(1,1) GARCH(1,1)的方差模型。而上述的正态性检验结果表明,残差的分布不适用标准正态分布,应该考虑其他类型的分布。 使用 r u g a r c h rugarch rugarch包对多个模型进行拟合。对于均值模型,考虑不带截距项的 A R I M A ( 4 , 0 , 4 ) ARIMA(4,0,4) ARIMA(4,0,4)。对于方差模型,阶数设定1阶ARCH和1阶GARCH,考虑标准GARCH( s G A R C H sGARCH sGARCH)、指数GARCH( e G A R C H eGARCH eGARCH)、 G J R − G A R C H GJR-GARCH GJR−GARCH、渐近幂ARCH( A P A R C H APARCH APARCH)、门限GARCH( T G A R C H TGARCH TGARCH)、非线性非对称GARCH( N A G A R C H NAGARCH NAGARCH)六类模型。对于残差分布类型,考虑标准正态分布( n o r m norm norm)、标准t分布( s t d std std)、偏t分布( s s t d sstd sstd)、广义误差分布( g e d ged ged)和Johnson’SU分布( j s u jsu jsu)五类分布。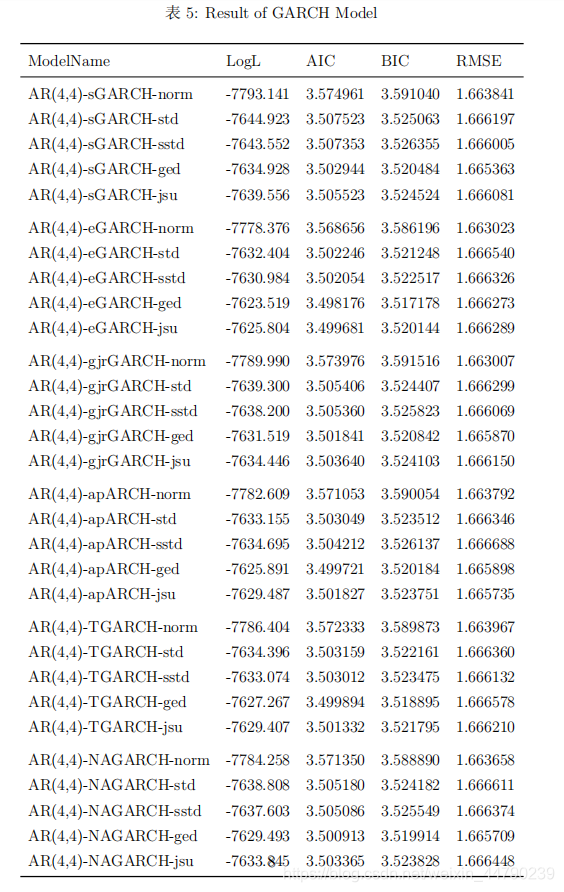 (二)模型比较
(二)模型比较
从拟合的模型结果来看,非对称类型的指数GARCH模型在最大似然估计值达到最大,同时AIC和BIC都能达到最小,说明指数GARCH模型比较好。从拟合的模型残差分布来看,非正态分布的AIC和BIC都明显低于正态分布,说明残差是服从重尾类型的分布。 选取指数GARCH模型,对比不同分布的参数显著性、检验结果以及模型效果,这里分布考虑正态分布、t分布、广义误差分布与三种分布对应的偏态分布以及Johnson’SU分布,结果如下所示。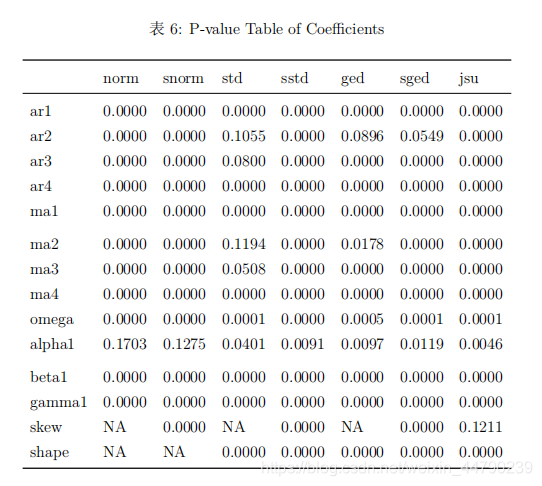 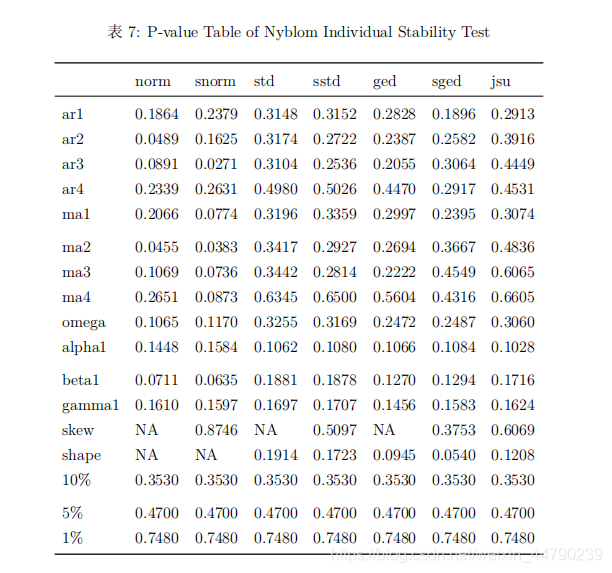 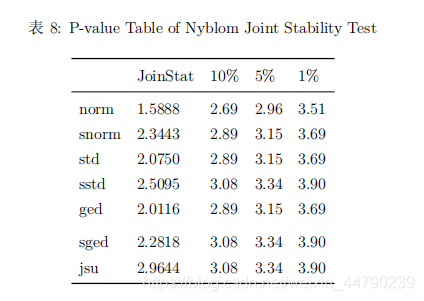 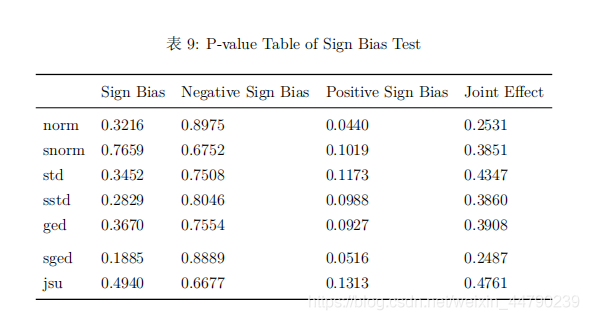 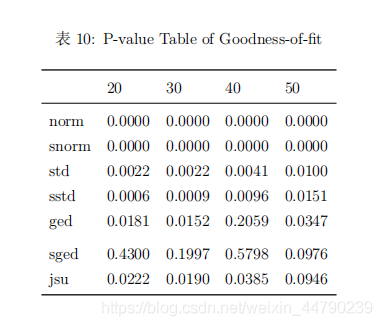 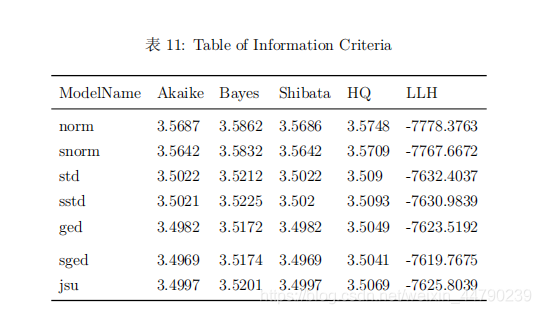
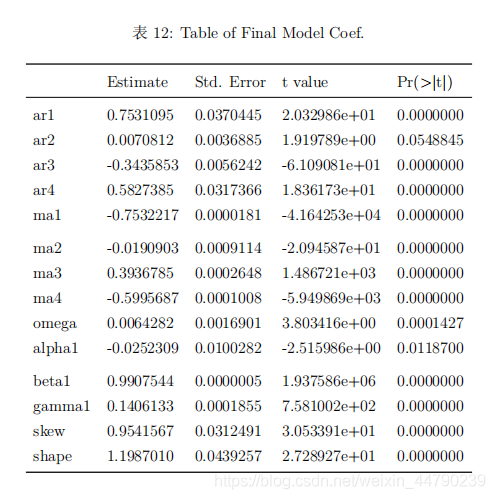
从模型拟合的系数显著性表可以看出,拟合的系数基本都显著,仅有少数参数不显著。从系数稳定性的个别检验和联合检验可以看出,在5%显著性水平下正态分布、偏正态分布、广义误差分布和偏广义误差分布都接收参数是稳定的原假设。从符号偏误检验的结果来看,指数GARCH模型正负残差的受到冲击的差异不明显,说明该非对称模型有效消除了杠杆效应。从调整皮尔逊拟合优度检验的结果来看,原假设是残差分布与理论分布没有差异,结果表明广义误差分布和偏广义误差分布是没有拒绝原假设,说明这两种分布与模型适配较好。 (三)模型选择 从模型拟合的信息准则表来看,偏广义误差分布的LLH达到最大,而BIC和HQ都达到最小,说明
A
R
M
A
(
4
,
4
)
−
e
G
A
R
C
H
(
1
,
1
)
−
S
G
E
D
ARMA(4,4)-eGARCH(1,1)-SGED
ARMA(4,4)−eGARCH(1,1)−SGED模型最优。拟合
A
R
M
A
(
4
,
4
)
−
E
G
A
R
C
H
(
1
,
1
)
−
S
G
E
D
ARMA(4,4)-EGARCH(1,1)-SGED
ARMA(4,4)−EGARCH(1,1)−SGED模型,理论模型和模型参数估计及显著性如下所示。
X
t
=
∑
i
=
1
p
φ
i
X
t
−
i
−
∑
j
=
1
q
ϑ
j
ε
t
−
j
+
ε
t
z
t
=
ε
t
σ
t
=
X
t
σ
t
l
n
σ
t
2
=
ω
+
α
z
t
−
1
+
β
l
n
σ
t
−
1
2
+
γ
(
∣
ε
t
−
1
∣
σ
t
−
1
−
E
∣
z
t
−
1
∣
)
其
中
,
ε
t
∼
S
G
E
D
(
0
,
1
,
s
h
a
p
e
,
s
k
e
w
)
\begin{aligned} X_t &= \sum \limits _{i=1}^{p}\varphi_i X_{t-i} - \sum \limits _{j=1}^{q} \vartheta_j \varepsilon_{t-j} + \varepsilon_t \\ z_t &= \frac{\varepsilon_t}{\sigma_t} = \frac{X_t}{\sigma_t} \\ ln\sigma_t^2 &= \omega +\alpha z_{t-1} + \beta ln\sigma ^2_{t-1} + \gamma (\frac{|\varepsilon_{t-1}|}{\sigma _{t-1}} - E|z_{t-1}|) \\ 其中,& \varepsilon_t \sim SGED(0,1,shape, skew) \end{aligned}
Xtztlnσt2其中,=i=1∑pφiXt−i−j=1∑qϑjεt−j+εt=σtεt=σtXt=ω+αzt−1+βlnσt−12+γ(σt−1∣εt−1∣−E∣zt−1∣)εt∼SGED(0,1,shape,skew) 本文通过对沪深300指数的波动性分析发现,我国股票市场有两段时间出现较大的波动。第一次波动出现在2008年前后,这段期间为全球金融危机,明显可以看出收盘价时序图出现明显的陡峭的波峰,持续时间较长;第二次波动出现在2015年前后,该阶段是由于杠杆资金的加入和政策收紧,形成短暂的牛市和熊市,波动程度不亚于2008年金融危机,但持续时间比较短。 本文使用多个GARCH模型进行比对,发现非对称模型 A R I M A − E G A R C H ARIMA-EGARCH ARIMA−EGARCH模型与沪深300指数的对数收益率有较高的匹配度,同时偏广义误差分布与理论分布较为接近,说明沪深300指数的波动性呈现的是尖峰厚尾、非对称性特征,说明我国股票市场存在杠杆效应。 六、实现代码 # Created by: Enguanei # Created on: 2021/5/7 # 导入包 library(knitr) library(pedquant) library(zoo) library(imputeTS) library(tseries) library(forecast) library(MTS) library(rugarch) library(dplyr) # 爬取网易财经的数据 datt |
【本文地址】
今日新闻 |
推荐新闻 |